

b) Using the result of part a, determine the moment of inertia of a circular area with respect to a diameter of the area. As with all calculations care must be taken to keep consistent units throughout. 4 Sample Problem a) Determine the centroidal polar moment of inertia of a circular area by direct integration. The above formulas may be used with both imperial and metric units. In this formula, Polar moment of inertia uses Outer Diameter of Shaft & Inner Diameter of Shaft.Notation and Units Metric and Imperial Units Here is how the Polar moment of inertia of hollow circular shaft calculation can be explained with given input values -> 3.988E-5 = (pi*(0.15^(4)-0.1^(4)))/32. For polar moment of inertia about an axis perpendicular to the x-y plane and. How to calculate Polar moment of inertia of hollow circular shaft using this online calculator? To use this online calculator for Polar moment of inertia of hollow circular shaft, enter Outer Diameter of Shaft (d o) & Inner Diameter of Shaft (di) and hit the calculate button. The polar moment of inertia of a circle is expressed as I 5 R 4 / 2.
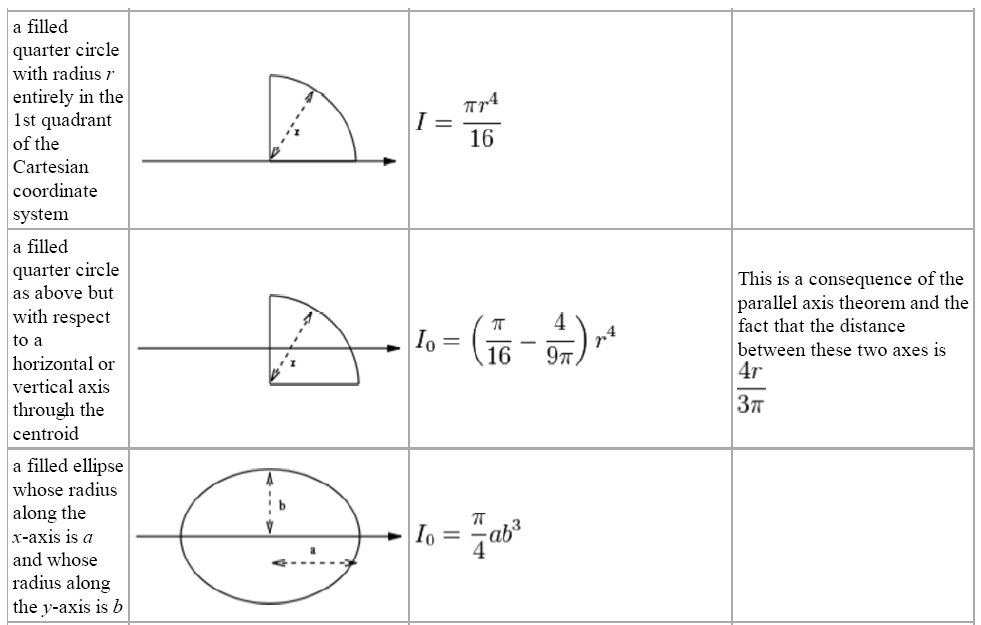
Similarly, a circle’s moment of inertia about an axis tangent to the circumference is given by I 5 R 4 / 4. The polar section modulus (also called section modulus of torsion), Zp, for circular sections may be found by dividing the polar moment of inertia, J. Polar moment of inertia is denoted by J symbol. It states that, The moment of inertia of a lamina about any axis parallel to the centroidal axis is equal to the Moment of inertia of the body about its centroidal axis plus the product of the area and square of distance between these two axes. This equation is equivalent to I D 4 / 64 when we express it taking the diameter (D) of the circle. Polar moment of inertia of hollow circular shaft calculator uses polar_momentofinertia = ( pi*( Outer Diameter of Shaft^(4)- Inner Diameter of Shaft^(4)))/32 to calculate the Polar moment of inertia, The Polar moment of inertia of hollow circular shaft formula is a quantity used to describe resistance to torsional deformation, in cylindrical objects (or segments of the cylindrical object) with an invariant cross-section and no significant warping or out-of-plane deformation.

How to Calculate Polar moment of inertia of hollow circular shaft?


 0 kommentar(er)
0 kommentar(er)
